고정 헤더 영역
상세 컨텐츠
본문 제목
[KMOOC-실습으로배우는머신러닝]4. Machine Learning with Optimization: Gradient Descent, Learning rate, Stochastic Gradient Descent, Momentum
본문
1️⃣ 최적화와 모형 학습
1-1. Machine Learning and Optimization
- Machine learning models optimize the function by minimizing the loss
- 머신러닝모델은 loss를 최소화함으로써 함수를 최적화한다.
- loss는 곧 실제값 - 예측값이다.
1-2. Linear Regression: 최적화의 중요성 알아보기
- 가장 기본적인 머신러닝 기법 및 통계적인 방법으로, input과 output사이가 선형관계임을 가정한다.
- loss function을 최소화함으로써 최적의 계수(coefficient, 베타를 결정한다.

👉 즉 linear regression함수의 구체적인 파라미터(베타)값을 부여해주려면 최적화과정이 필요하다.

1-3. Loss Function or Neural Networks
- We cannot optimize the funstion analytically
- 굉장히 복잡하다! 굉장히 고차원에 있다!
2️⃣ 경사하강법개요
2-1. INTRO) Iterative Algorithm-based Optimization
경사가 있는 산 혹인 비탈길에서 내려온다고 생각하자. 보폭을 크게하든, 작게하든 반복되는 스텝으로 땅 밑까지 내려오는 과정을 비유해보면 즉 어떤 루프나 일련의 스텝들을 반복하여 최적화된 지점을 찾아가는 방법이라고 설명할 수 있다.
2-2. Gradient Descent
- 가장 대표적인 iterative algorithm이다.
- 여기서 Gradient는 기울기로, Loss가 빠르게 작아지는(즉 함수값이 작아지는) 방향을 찾고, 그 방향으로 한발자국씩 계속 내려가는 방법이다.
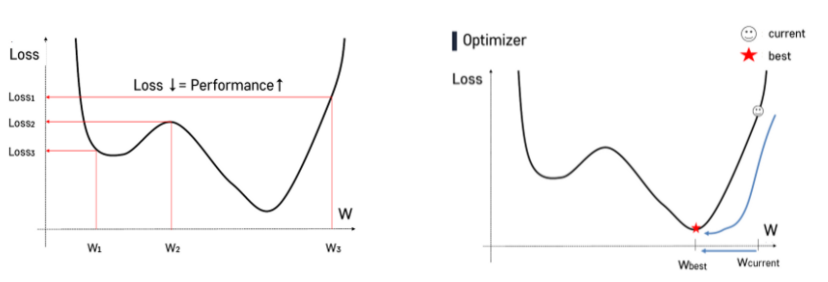
- current → best로 나아가는 과정이며 이때 w는 random으로 initialize한다
하지만 함수가 복잡하기 때문에 디테일한 기울기 변화를 알 수 없다.
- Brook Taylor의 테일러 급수전개: 모든 일반적인 함수의 경우에는 무한대로 수렵하는 다항식의 근사가 가능하다
- Quardratic approximation(2차다항식으로의 근가) → Gradient Descent

- 회색 선에 원래 수식에 대한 그래프라면, 이를 Quardratic approximation한 것이 검은색 선으로 표현된 그래프이며, 이를 나타는 수식이 가장 위에 있는 수식이다. w는 기울기이며, w에 대해 0이 되는 지점을 찾는다.
3️⃣ 경사하강법 심화
3-1. Learning Rate

t는 기울기이다. t의 크기에 따라 함수의 모양이 변하고, 업데이트 정도가 달라진다. 따라서 우리는 이를 조정해야하는 하이퍼파라미터라고 볼 수 있다.
이 하이퍼파라미터를 step size 또는 learning rate이라 하기도 한다. 특히 learning rate은 머신러닝에서 Gradient descent를 말할때 자주 사용한다.
- learning rate이 잘 설정되어있다면, 몇번의 과정을 거치치 않고 최소점으로 이동할 수 있다.
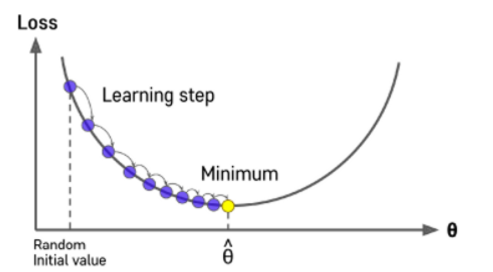
- learning rate이 너무 작으면 줄어드는 속도가 오래걸린다.

learning rate=”adam”이라고 하면 경우에 따라 learning rate을 adaptive하게 조절해준다.
- learning rate이 너무 크면 loss값이 발산해버린다

3-2. Stochastic Gradient Descent(SGD)
- Consider minimizing an average of functions
데이터가 너무 클 경우 데이터를 분할하여 각 batch마다 gradient descent를 해 업데이트를 해나가는 방식이다. 일종의 추정하는 gradient descent라 할 수 있고, 효율적인 방법이다.
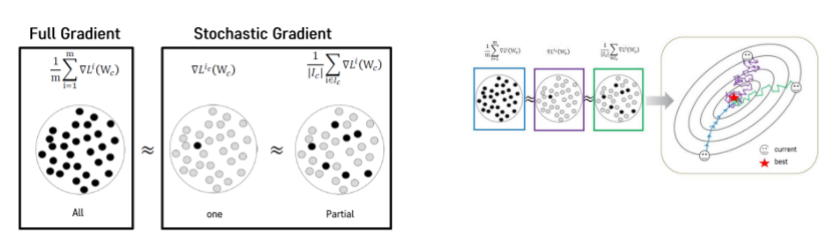
어느정도 사이즈가 있는 batch사이즈를 갖는 것이 좋으며 특히 Deep learning에서는 이 방법을 많이 사용한다.
오른쪽 그림에서 파란색 선이 Full Gradient, 초록색이 partiral한 Stochastic Gradient이다. 파란색 선은 정확하고 빠르게 best를 찾아가지만 적은량의 데이터를 샘플링할수록 Gradient Descent가 조금씩 어긋남이 보이나 그래도 최적의 해로 수렴해간다.
또한 Full Gradient가 한번 업데이트되는 동안 partiral한 Stochastic Gradient는 배치의 개수만큼 업데이트가 일어나게 된다. 따라서 훨씬 빠르게 해를 구할 수 있다는 장점이 있다. 따라서 SGD는 빅데이터에서 많이 사용한다.
3-3. Global vs Local Minimum

Local minimum은 극솟값을 뜻하며, Global minimum은 Local minimum 중 가장 작은 값을 뜻한다. 일반적으로 Gradient Descent를 하면 Local minimum을 찾는 것은 확실히 보장되지만, Global minimum을 찾는 것은 확실히 보장될 수 없다.
3-4. Momentum
n. 과거에서 업데이트 해왔던 방식을 계속 기억하는 것
문제는 Gradient Descent를 사용하면 Local minimum에 수렴하긴 하나 이를 벗어나지 못하며 이것이 Global minimum이라는 보장은 없다.

따라서 Local minimum을 뛰어넘어 더 작은 값들을 찾아가는 계기를 만들어 주기 위해 Momentum이 적용된다. 다시 말하면 더 최소점에 도달할 수 있도록 최솟값을 찾아온 방향을 관성으로 기억하여 앞으로 더 나아가 최솟값을 찾을 수 있도록 도와주는 방법이다.
일반적으로 기울기는 0이지만 앞뒤 혹은 양 옆의 기울기가 변함이 없는 Saddle point나 Local minimum으로 빠르게 수렴한 경우 이 point들을 넘어서 더 최적점을 찾을 수 있도록 도와준다.
👉 결론적으로 SGD + Momentum이 딥러닝에서 가장 많이 사용되는 방법이다.
'멋사 AISCOOL 7기 Python > INPUT' 카테고리의 다른 글
| [KMOOC-실습으로배우는머신러닝] 7.Ensemble Learning (0) | 2022.11.22 |
|---|---|
| [KMOOC-실습으로배우는머신러닝] 5. Support Vector Machine (0) | 2022.11.22 |
| [KMOOC-실습으로배우는머신러닝]2. Machine Learning Pipeline (0) | 2022.11.21 |
| [KMOOC-실습으로배우는머신러닝] 1. Introduction to Machine Learning (0) | 2022.11.21 |
| [머신러닝] Titanic 데이터를 사용한 분류: Feature Engineering(결측치 보간법) + 하이퍼파리미터튜닝(RandomizedSearchCV) (0) | 2022.11.17 |




